Quantum Annealing with examples

Created by Valter Uotila

Unified Database Management Systems

lead by Jiaheng Lu

Problem: modern database management systems do not have a solid theoretical foundation.

Oracle started promoting category theory as a theoretical foundation for various database concepts.

Category theory is very applicable: we published some results in VLDB'21 and its workshops.

Applied category theory for multi-model databases

Motivation

Quantum computing does not yet outperform classical computers in real-life applications but...

...it might be more sustainable to operate and ...

... we can avoid making ethical mistakes. For example, see Gender BIAS in AI: Perspectives of AI Practitioners.

Quantum Annealing

Implementation by

Initial paper in Nature: Quantum annealing with manufactured spins

Motivation for quantum annealing

D-wave has many examples of use cases:

General idea

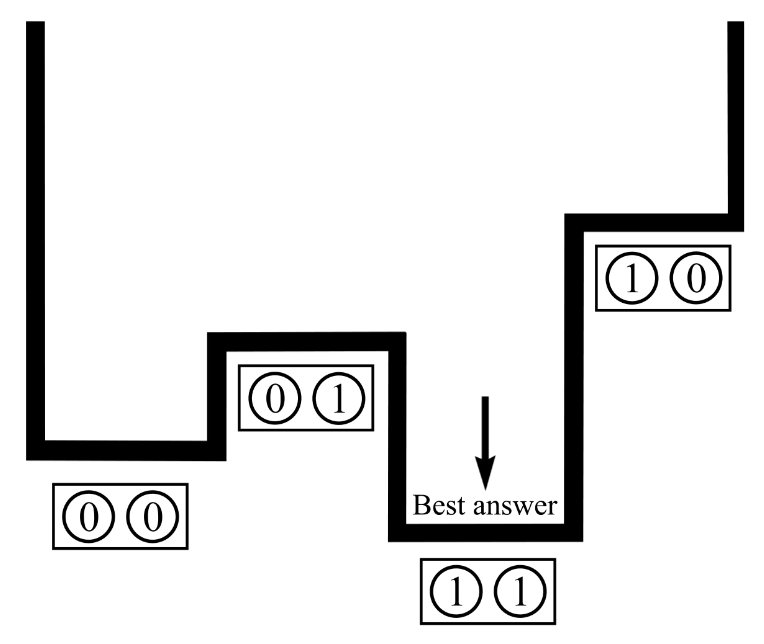
Goal: finding the global minimum of a given objective function

Simulated annealing on classical hardware

Annealing process: bias

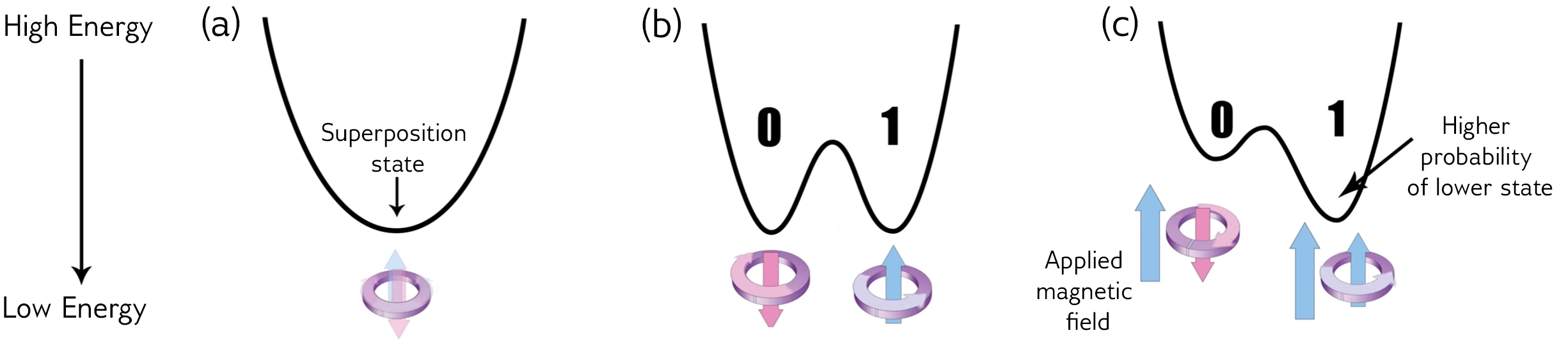
Annealing process: couplers

Studies about performance of quantum annealing

Google studied that quantum annealing outperforms simulated annealing

General study: Performance of quantum annealing hardware

Important paper

Ising formulations of many NP problems

by Andrew Lucas

Example: Steiner trees

\[\begin{aligned} H_{A} & = A\left( 1 - \sum_{v}x_{v,0} \right)^2 + A \sum_{v \in U} \left( 1 - \sum_{i}x_{v,i} \right)^2 \\ & + A \sum_{v \notin U} \left( y_v - \sum_{i} x_{v,i} \right)^2 \\ & + A\sum_{v}\sum_{i = 1}^{N/2}\left(x_{v,i} - \sum_{(uv) \in E}x_{uv,i} \right)^2 \\ & + A \sum_{uv \in E}\left( y_{uv} - \sum_{i}(x_{uv,i} - x_{vu, i}) \right)^2 \\ & + A\sum_{uv, vu \in E}\sum_{i = 1}^{N/2}x_{uv,i}(2 - x_{u,i-1} - x_{v,i}) \end{aligned} \]

Relationship to gate-model

Qiskit Workshop at Aalto

Compared to other paradigms

Quantum computing companies with different paradigms and hardware

Demonstration:

Sudoku

BMW quantum computing challenge:

Sensor positions optimization

Problem

Cars, especially self-driving cars, require multiple sensors to monitor the car's environment. Positioning the sensors is a combinatorically difficult problem and testing different combinations is slow.

In this challenge BMW wanted to research possibilities of quantum computing in the sensor positioning process.

New Angles from Right Range:

Optimizing Car Sensor Positioning with D-Wave Hybrid Quantum Computers

Valter Uotila & Sardana Ivanova

Core idea of solution

We utilized Quadratic Unconstrained Binary Optimization model and followed the standard approach in D-wave's examples and in the paper Ising formulations of many NP problems.

Core idea of solution

  • Formalizing problem
  • Defining suitable binary variables
  • Identifying and creating suitable constraints
  • Implementing variables and constraints with Ocean software framework

Jupyter notebook containing solution draft

Future work

Quantum computing for databases

Overall two-level picture

"Easy" level

Solving classical database optimization and modeling problems with quantum computing

Problem: quantum computing might not scale and bring any benefits

Join order optimization

Problem: for a given subset of vertices, select a subset of vertices and edges so that they all together form a tree and the total weight is minimized.
Possible solution: Express the problem using Steiner trees and implement using the idea in the paper Ising formulations of many NP problems.

"Hard" level

Will we be able to store and query quantum data from quantum databases?

What does it mean?

How would it work?

Why do we need it?

Category theory & quantum computing:

Conclusion

Thank you for your interest and the opportunity to give a presentation!

Questions, comments, dicussion?

This presentation is created using

The HTML Presentation Framework

Created by Hakim El Hattab and contributors