Quantum computing perspective for (Big) Data management
Valter Uotila
January 30, 2023
Second year PhD student at the Unified Database Management Systems research group
Supervised by professors Jiaheng Lu and Jukka K. Nurminen
My previous focus was in category theory applied to multi-model databases -- now the topic is extended with quantum computing
Quantum computing and information processing

Plethora of different kinds of computing devices and computing models besides ordinary CPUs
- Abacus (counting frame)
- GPUs
- TPUs
- DNA computing
- Processors in Minecraft
and quantum computers.
Quantum computing works on various hardware
Although the hardware varies the abstract model of quantum computing is quite standard (circuit):
- IQM (circuit)
- IBM (circuit, superconductor)
- Google (circuit, superconductor)
- IonQ (circuit, trapped ion)
- Honeywell with Quantinuum (circuit, trapped ion)
- Rigetti (circuit, integrated)
- Microsoft (circuit, topological?)
- Xanadu (circuit, photonic)
- D-wave (annealing & circuit coming)
Why does it work?
The abstract foundation of quantum computing is based on quantum mechanics.
See section Introduction to quantum mechanics in book Quantum Computation and Quantum Information 10th Anniversary Edition by Nielsen and Chuang.
Approaching from machine learning perspective
You have developed a machine learning model to classify cats and dogs.
Model outputs that the image has 80% prob of represeting cat and 20% prob of representing a dog.
Approaching from machine learning perspective

If you modify the model, you want:
the prob of cat + the prob of dog = 100%
Making things more abstract:
Instead of cats and dogs, we have vectors.
Instead of probabilites, we have complex numbers which implicitly encode the probabilities.
Single qubit systems
$|\psi\rangle = \alpha|0\rangle + \beta|1\rangle$
where $\alpha,\beta \in \Complex$ are amplitudes and
$|\alpha|^2 + |\beta|^2 = 1$.
The states $|0\rangle = \begin{bmatrix} 1 \\ 0 \end{bmatrix}$ and $|1\rangle = \begin{bmatrix} 0 \\ 1 \end{bmatrix}$ are called computational basis.
Multiple qubits
\[\begin{aligned} |\psi\rangle &= (a_0|0\rangle + b_0|1\rangle) \otimes (a_1|0\rangle + b_1|1\rangle) \\ & = a_0a_1|00\rangle + a_0b_1|01\rangle + b_0a_1|10\rangle + b_0b_1|11\rangle. \end{aligned} \]
We see that $n$ qubit system has $2^n$ amplitudes (i.e. the coefficients).
Evolution of quantum systems
Initial system of qubits (usually $|00\ldots0\rangle$)
Apply gates the qubits. Gates are modelled as unitary matrixes. The idea is that the sum of the squared norms of complex amplitudes is preserved.
Measure the system. The system ends up to some classical state. The sequence of classical bits is the result of the quantum computation.
Two big advantages of quantum computing
Superposition
One qubit can be in multiple states simultaneously.
For example, the most common method to put a qubit to a superposition is to apply Hadamar-gate
$H|0\rangle = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}\begin{bmatrix} 1 \\ 0 \end{bmatrix} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \frac{|0\rangle + |1\rangle}{\sqrt{2}}$.
Entanglement
Entanglement roughly means that two or more qubits are connected and they can interact in ways such that the state of each qubit cannot be described independently of the state of the other qubits.
For example, the most common method to entangle two qubits is to use CNOT gate:
CNOT$(|x\rangle \otimes |y\rangle) = |x\rangle \otimes |x + y \mod 2\rangle$.
Some challenges in quantum information processing
that are related to "data"

No-cloning theorem
Theoretically provable theorem that quantum states cannot be copied or cloned.
See Box 12.1: The no-cloning theorem in book Quantum Computation and Quantum Information.
Measuring destroys states
Measuring a qubit collapses it to either 0 or 1. After the measurement we cannot modify the measured qubit anymore.
Error
Quantum computing is never performed in absolutely isoleted system and the environment creates decoherence and other quantum noise.
We can tackle the error by developing quantum error correction.
Quantum annealing
Quadratic Unconstrained Binary Optimization (QUBO) on quantum annealers
Implementation by

Initial paper in Nature: Quantum annealing with manufactured spins
Motivation for quantum annealing
D-wave has many examples of use cases:
General idea
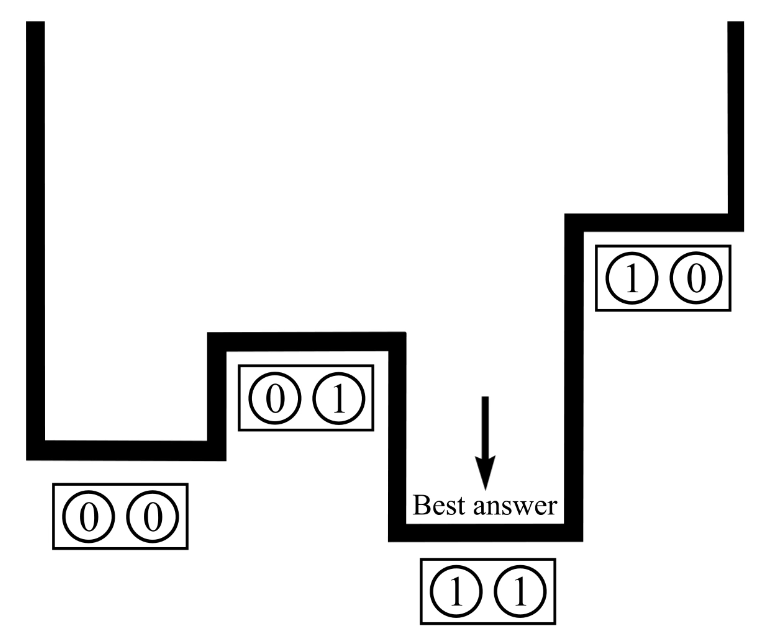
Goal: finding the global minimum of a given objective function
Simulated annealing on classical hardware

Annealing process: bias
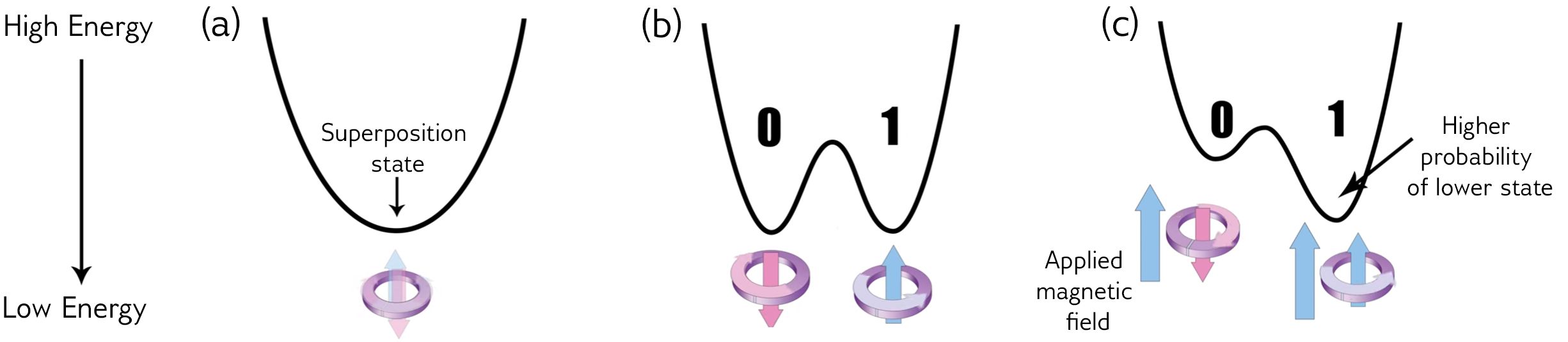
Annealing process: couplers
Relationship to circuit-model
What kind of database problems are we tackling with quantum computing?
The research plan published in: Uotila, Valter . Synergy between Quantum Computers and Databases . in Proceedings of the VLDB 2022 PhD Workshop co-located with the 48th International Conference on Very Large Databases (VLDB 2022), 05/09/2022 . http://ceur-ws.org/Vol-3186/paper_1.pdf
Solving classical database optimization and modeling problems with quantum computing
- SQL2Circuits: Predicting metrics for SQL queries with quantum natural language processing method (ongoing)
- Optimizing task and virtual machine allocation (ongoing)
- Join order optimization (near future)
- Size bounds for conjunctive queries (future)
- Transaction scheduling (collaboration work)
Problem: quantum computing might not scale and bring any benefits
SQL2Circuits: Predicting metrics for SQL queries with quantum natural language processing method
Transformation of SQL queries into parametrized circuits based on their context-free grammar representation
Optimizing circuit parameters so that the framework could predict execution times and cardinalities
Optimizing task and virtual machine allocation
Quantum annealing -based QUBO formulation for task and virtual machine allocation to physical machines in data centers
We are taking into account energy consumption and sustainability metrics
Uotila, Valter and Lu, Jiaheng. Quantum Annealing Method for Dynamic Virtual Machine and Task Allocation in Cloud Infrastructures from Sustainability Perspective. SMDB 2023 Workshop. In review.
Join order optimization
One of the most classical database problems: find the optimal way to join relational tables
Already has a QUBO formulation but the formulation is not spesific for this problem: we aim to find specific QUBO formulation
As a conclusion, quantum computing will not yet reshape database field
The current hardware has limited capabilites.
But quantum computing offers many interesting promises which we research:
- computational speedup
- new methods to develop and design novel algorithms
- hybrid frameworks
- quantum machine learning is a big topic
- probably lower energy consumption
Thank you for your interest and the opportunity to give a presentation!
Questions, comments, dicussion?
This presentation is created using

The HTML Presentation Framework
Created by Hakim El Hattab and contributors
